허프 변환(Hough Transform)의 개념 및 구현 + 내 생각

05 Jan 2017

Reading time ~7 minutes

허프 변환(Hough Transform)

예전에 영상처리를 잠깐 공부한 적이 있었는데 허프 변환이 생각보다 간단한 내용임에도 불구하고 너무 어렵게 설명되어 있는 곳이 많았다. 그래서 그 내용을 네이버 블로그에 올렸던 적이 있었다. 근데 이 글이 반응이 꽤 괜찮았어서, 이 블로그에 그 내용을 좀더 정리해서 옮겨 볼까 한다.

이 글은 전반적인 이해를 원하는 사람 보다는 허프변환을 실제로 구현하려는 사람 혹은 허프변환의 기초에 대해 완전한 이해를 하고 싶은 사람 을 위한 글이다.

허프변환의 기본 아이디어는 이렇다.

한 점(x1,y1)가 가질수 있는 직선은 y1 = m*x1 + b 이다.

이 점을 m, b 에대한 식으로 표현하면, b = -m*x1 + y1 처럼 직선으로 표현할수 있다.

즉, 한 점이 가질 수 있는 모든 직선을 b와 m에 대한 평면에서 하나의 직선으로 표현할 수 있다.

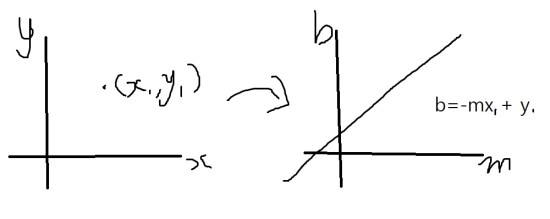
hough_transform

그렇다면 생각해보자 두 점을 m,b에 대한 식으로 바꿨을때는 m,b평면에서 직선이 두개 나오게 된다.

그렇다면 그 두 직선의 교점은 무엇을 의미할까? 바로 두 점을 지나는 직선을 의미 하게 된다.

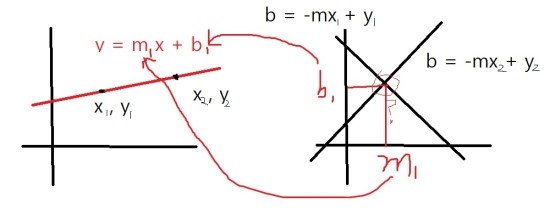
cross

왜냐고? m,b평면에서 나타낸 직선은 한 점이 가질 수 있는 모든 직선을 의미하고 m1,b1 에서 만난 점

은 두 점이 모두 가질 수 있는 직선을 의미하기 때문이다.

자 이제 두 점이 아닌 윤곽선들을 대상으로 해보자.

각각의 수많은 점들은 m,b 평면의 수많은 직선으로 옮겨지게 되고, 이 직선들은 많은 교점이 있을 것

이다. 그 교점이 의미하는 것이 뭐라고? x,y 평면에서 그 점들을 지나는 직선! 을 의미한다는 것. m,b

평면의 한점은 x,y평면에서의 직선이기도 하지않은가?

그렇다면 그 직선들의 교점(m1,b1)에 겹치는 직선들이 많으면 많을수록 그 영상에는 y = m1*x + b1 라는 직선이 존재할 가능성이 높아진다는 것을 의미하는 거다.

그래서 m,b 공간의 교점들을 검사해 (구체적으로 어떻게 검사하는 지는 나중에 설명) 그 값이 임계치(threshold, 임의의 값)보다 높으면 그 직선을 검출한다.

이것이 허프변환의 기본 개념이다. 넘 어렵게 설명했나.. 그런데 하나하나 곱씹으며 생각해보면 그리

어렵지 않은 개념인 것을 알 수 있다.

그런데 막상 실제 구현에 사용하게 되려면 문제가 있다는 것을 쉽게 알 수 있다.

실제 구현에서는, m,b 평면을 ‘배열’로 표현해서 그 직선에 해당하는 m,b를 누적하고 사용하게 되는

데, 배열은 ‘유한’한데,직선이 y축과 평행 할 경우, 기울기, 즉 m은 무한대의 범위이므로 문제가 있다는 것을 알 수 있다.

m,b를 누적하고 사용한다는 의미는 뭘까. 우리가 평면에 직선을 긋는다면 실제로 메모리 상에 긋는다

고 생각할 것이 아니라 당연히 배열로 표현을 한다. 예를 들어 m,b평면에서 y = x 라는 직선이 있으면

배열의 대각선의 원소에만 1을 더하는 개념이 되겠다. 그렇다면 y = 2x라는 직선이 있을때, 약 75도의

기울기의 원소에 1을 더할 것이고, y = x의 교점. (0,0)은 원소가 2가 될 것이다!

따라서, 유한한 크기의 배열을 비교하면서 숫자가 임계치보다 높으면 그 m,b값에 해당하는 y=mx +b

직선이 검출되었다는 것을 확인 할 수 있다.

임계치는 맘대로 정할수도 있겠지만 임계치를 구하는 알고리즘은 어떻게 될까 생각해 보자.

난 귀찮아서 구현을 안했지만 이것도 구현하는게 훨씬 인식률이 좋기 때문에 구현하는 걸 추천.

자 이제 좀 전으로 돌아가면. m,b평면은 문제가 있다고 했다. 바로 배열은 ‘유한’한데, 기울기(m)은 ‘무

한’ 하다는 것. 우리는 ‘무한’->’유한’으로 바꾸어 줄 필요가 있다. 그래서 생긴게 뭐?

바로 Hough Space.(허프 공간)이다.

이건 걍 무한->유한 으로 바꾸어 주기 위한 장치일뿐 m,b평면과 비슷한 개념으로

생각하면 된다. 허프 공간은 아래와 같다.

r = xcost + ysint

허프 공간

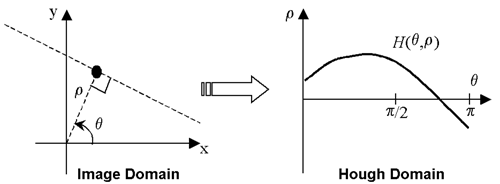
위 그림에서 theta가 t이다.

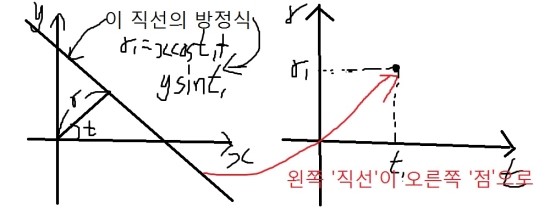
hough_space

오른쪽에 있는 t와 r에 대한 평면이 Hough Space이다. 위에서 설명한 m,b평면과 개념이 완전히 똑같다. 단지 다른점은 공간이 ‘무한’한 상태에서 ‘유한’한 상태로 바뀌었다 는 것뿐.

왜 유한할까 생각해보자. r은 어디까지 유한 할까? 바로 비트맵의 대각선 길이(d라고 하자)까지이다.

즉, 범위는 0<r<d이다. 그렇다면 t는 범위가 어디까지일까? 바로 -90도 부터 180도까지이다.

그 이유에 대해서 설명 해보면, 다시 위의 사진중 왼쪽 그림을 보자. 우리가 검출하는 직선은 왼쪽 그래프의 1사분면, 그 중에서도 0<x<화면 너비, 0<y<화면 높이에 있다. 그럼 만약 r이 화면 대각선의 길이보다 크다고 하면, 그 직선이 화면에 표시가 될까? 그렇다 안되기 때문에 그건 의미가 없는 것이고, 우리는 의미있는 직선만을 계산하겠다는 것이다. t의 범위가 -90도 부터 180도 인 이유도 마찬가지다. 과연 t가 180도 ~ 270도 사이일 때, r값이 몇이던지 간에 직선이 1사분면에 표시될 수 있을까? 없다. 따라서 범위가 180도 ~ 270도 사이인 것은 계산할 필요가 없다.

자, 결국 우리는 픽셀 외곽선의 모든 점들이 가질 수 있는 직선들을 Hough공간에 누적시킬 수 있게 되었다.
한번 선언해 볼까 int HoughS[d][270] = {0}; 이다. d는 위의 설명을 잘 읽었다면 잘 이해가 갈 것이고,
270인 이유는 배열을 사용해서 -90 < t < 180을 표현하기에는 무리가 있으니 -90도에서 0도 부분은 180도 에서 270도로 표현하는 것이다.

어쨋든 여기에 누적 시키면 되고, 누적 시킨 값들을 검사하여 임계치 이상의 값을 가지고 있으면 그 r,t

값을 다시 x,y공간으로 변환하여(변환하면 당연히 직선이 되겠지?) 표현 해주면 된다.

다시 x,y공간으로 변환하는 간단한 과정도 생각이 안난다는 사람을 위한 팁

r = xcost+ysint 니까!

x = (r-ysint)/cost ! 여기서 y를 1씩 증가시키며 x를 구한다음에 x,y공간에 표현해주면 되겠지요

y = (r-xcost)/sint ! 여기선 x를 1씩 증가 이다.

그런데 왜! x를 1씩증가시키며 구한 y값을 똑같은 식인데 왜 y도 1씩 증가시키며 x를 구할까?

x를 증가하며 y를 구했을때 직선이 45도 이상에서는 y가 급격하게 늘어나 중간에 빈 공간이 생기는 현상이 생긴다.

이러한 현상이 일어나는 이유는, 화면 상에는 선을 긋는다라는 개념은 컴퓨터 상에선 height*width의 비트맵에 특정좌표(x,y)에 점을 연속적으로 그리는 행위라고 말할 수 있다.

그렇다면 컴퓨터의 입장이 되어서 종이에 격자를 그려놓고 y=2x를 그려보자.

단순히 x를 꾸준히 증가시키고 그 값에 따라 좌표를 찍게 되면 중간중간에 빈공간이 생기게 된다.

예를 들어 y가 3일 경우에는 점이 찍히지 않는다. 그래서 x뿐만아니라 y를 꾸준히 증가시켜 그 빈공간을 채우는 일을 한다는 의미이다.

사실 이 내용만 딱 보고서 소스를 쨔보는 걸 강력히 추천한다. 그리고 실제로 테스트 해보고, 문제점이

뭔지, 어떻게 하면 좀 더 나은 인식률을 가질 수 있는지 생각해 보고 밑에 소스를 보는 것을 추천한다.

왜냐면 내가 쨘게 정답이 아니고 내가 알고 있는 걸 최대한 쨔보고 해결 방안도 생각한 것이기에 더

나은 방법이 있고 쩌는 방법이 있다면 그게 더 나은 알고리즘이고 공유좀 하길 원한다

#define BITMAP_WIDTH 800
#define BITMAP_HEIGHT 600

#define IMAGE_DIAGONAL sqrtf(BITMAP_WIDTH*BITMAP_WIDTH + BITMAP_HEIGHT*BITMAP_HEIGHT) //대각선의 길이

#define THETA 270
#define LINE_THRESHOLD 40
#define SHARP_THRESHOLD 5

void HoughTransform(LPBYTE* outImage,LPBYTE* inputImage,int nW,int nH)
{
 register int i,j,k,l,m;
 int d;
 float p2d = 3.141592654f/180.0f;

 int thres = 20;

 for(i=0;i< IMAGE_DIAGONAL;i++)
 {
  for(j=0;j<THETA;j++)
   H[i][j] = 0;
 }

 float *LUT_COS = new float[THETA];
 float *LUT_SIN = new float[THETA];
 float *LUT_COT = new float[THETA];
 float *LUT_SEC = new float[THETA];

 for(i=0;i<THETA;i++)
 {
  LUT_COS[i] = cosf((i)*p2d);
  LUT_SIN[i] = sinf((i)*p2d);
  LUT_COT[i] = 1/tanf(i*p2d);
  LUT_SEC[i] = 1/LUT_SIN[i];
 }

 for(i=0;i<nH;i++)
  for(j=0;j<nW;j++)
   if(inputImage[i][j] > SHARP_THRESHOLD)
   {
    for(k=0;k<THETA;k++)
    {
     d = (int)(i*LUT_COS[k] + j*LUT_SIN[k]);

     if( d >= 0 && d < IMAGE_DIAGONAL )
      H[d][k] += 1;
    }
   }
  }
 }
 for(i=0;i<nH;i++)
 {
  for(j=0;j<nW;j++)
   outImage[i][j] = 0;
 }
 int w = 0;
 int max_w = w;
 float theta_thres = 0.1;
 double const PI = 3.1415926535;
 for(d=0;d< IMAGE_DIAGONAL;d++)
 {
  for(k=0;k<THETA;k++)
  {
   if(H[d][k] > thres)
   {
    int max = H[d][k];

    /*
      윤곽선을 검출을 하게되면 실제로 두껍게 감지되기 때문에,
      직선도 여러줄이 감지가 되게 된다.
      여러줄이 감지가 되는것을 방지하고 감지된 직선을 얇게 하기 위해서 밑의 코드를 삽입
    */
    for(l=-4;l<4;l++)
    {
     for(m=-4;m<4;m++)
     {
      if(d+l>=0 && d+l< IMAGE_DIAGONAL && k+m >= 0 && k+m < 180)
      {
       if(H[d+l][k+m] > max)
        max = H[d+l][k+m];
      }
     }
   }

    if(max > H[d][k]) continue;
    //if((k <= 45 && k <= 315) || (k >= 135 && k <= 225))
    {
     for(j=0;j<nW;j++)
     {
      i = (int)((d-j*LUT_SIN[k])/LUT_COS[k]);

      if(i < nH && i > 0)
      {
       if(inputImage[i][j] > SHARP_THRESHOLD)
        w++;
       else
       {
        if(w > max_w)
         max_w = w;
        w=0;
       }
      }
     }
     if(max_w > LINE_THRESHOLD)
     {
      for(j=0;j<nW;j++)
      {
       i = (int)((d-j*LUT_SIN[k])/LUT_COS[k]);

       if(i < nH && i >= 0)
       {
        //if(inputImage[i][j] > SHARP_THRESHOLD)
        outImage[i][j] += 1;     
       }
      }
     }
    }


    //if(LUT_COT[k] <= 3.141592/4 && LUT_COT[k] >= 3.141592*5/4)
    //else
    {
     w = 0;
     max_w = w;
     for(i=0;i<nH;i++)
     {
      j = (int)((d-i*LUT_COS[k])/LUT_SIN[k]);

      if(j < nW && j > 0)
      {
       if(inputImage[i][j] > SHARP_THRESHOLD)
        w++;
       else
       {
        if(w > max_w)
         max_w = w;
        w=0;
       }
      }
     }
     if(max_w > LINE_THRESHOLD)
     {
      for(i=0;i<nH;i++)
      {
       j = (int)((d-i*LUT_COS[k])/LUT_SIN[k]);

       if(j < nW && j >= 0)
       {
        //if(inputImage[i][j] > SHARP_THRESHOLD)
        outImage[i][j] += 1;

       }

      }
     }
    }
   }
  }
 }
 delete []LUT_COS;
 delete []LUT_SIN;
 delete []LUT_COT;
 delete []LUT_SEC;
}

** 위의 소스에는 약간의 응용이 들어가 있다.

허프 변환에는 실제로 해봤을 때 생각보다 직선이 아닌것도 직선이라고 판단을 많이 한다. 왜일까?

실제로 prewitt이나 sobel mask들을 적용 했을때 윤곽선만 정확히 따는 것이 아니라 잡음들을 꽤

많이 따는 것을 알 수 있다. 잡음이 많다는건 허프변환에서 직선인지 아닌지 판단하는 점들이 많다는

것이고, 그 잡음 점들이 일직선 상에 띄엄띄엄 있게되고 그게 임계치를 넘게되면 이걸 직선으로

판단해버린다 ㅋ

그래서 낸 대안이 바로 점들이 연속되게 일직선으로 있느냐(직선이 끊기지 않는 직선이냐)를 판단하는 것이다.

위의 소스를 보면 그걸 구현 해놨다. 사실 누구나 생각 할 수 있는 건데 그래도 내가 아는 걸 최대한 써보려고 써봄

image-processing C/C++영상처리