인터넷 상에 돌아다니는 P,NP에 관한 글들은 나에겐 굉장히 어렵게 느껴졌다.(P-NP에 관한 글은 쉽게 적혀있어도, co-NP, NP-Hard, NP-complete에 관한 문제는 이해하기가 쉽지가 않다.)
원래 가볍게 알고 넘어가려 했지만, 워낙에 중요한 개념이기도 한데 자료들 대부분이 어렵고 애매하게 정리되어 있어서, 명확하게 정리해두면 좋을 것 같아 글을 작성했다.
P - NP 문제
의의
P-NP 문제를 알기 전에, 도대체 왜 이런걸 알아야 하는지에 대한 의문을 제기할 수 있다.
P-NP 문제는 어떤 문제가 주어졌을 때 어렵다, 쉽다를 결정하는 기준점 을 제시한다. 어렵다, 쉽다의 개념은 상대적인 개념이기 때문에, 특정 기준점을 제시해 문제 해결에 좀 더 효과적인 공략을 해보자!는 것이 P-NP 문제의 의의다.
참고로 P - NP문제는 수학계의 최대 난제인 7대 밀레니엄 문제 중 하나이다. P=NP를 증명하거나, P!=NP를 증명하게 되면, 약 12억의 상금과 튜링상 수상 및 모든 컴퓨터과학 업계를 뒤흔들 수 있다.
요약
- P 문제(Polynomial problem) :
결정론적 튜링머신으로 다항시간 내에 풀 수 있는 문제 - NP 문제(Non-deterministic Polynomial problem) :
비 결정론적 튜링머신으로 다항시간 내에 풀 수 있는 문제
튜링머신과 다항시간을 기반으로 P-NP문제를 설명 했으니, 이제 각각이 무엇인지에 대해서 설명해보자.
다항 시간(Polynomial Time)
다항시간 내에 풀 수 있다는 의미는, 시간 복잡도가 O(n^2), O(n^3)같이 O(n^k)로 표현될 수 있다 는 의미이다.
시간복잡도는 문제를 해결하는데 걸리는 시간과 입력의 함수 관계를 말한다. 즉, 특정 문제가 주어졌고, 그 문제에 n=100이라는 입력이 들어왔을 때, 그 문제를 해결하는데 100*100의 시간이 걸렸다면 시간복잡도는 O(n^2)로 표현할 수 있다. 만약 해결하는데 2^100의 시간이 걸렸다면, 시간복잡도는 O(2^n)으로 표현할 수 있다.
다항시간에 풀 수 있는 문제의 예시로는 정렬 문제가 있다. 길이가 n인 데이터가 주어졌을 때, 병합 정렬 등을 이용하면 O(nlog(n))의 시간복잡도로 문제를 해결할 수 있다고 증명되었다. 즉, 학생 100명의 이름이 적힌 출석부를 컴퓨터에 입력하면 컴퓨터는 약 100log(100)번의 연산만 하면 학생 이름을 정렬해서 보여줄 수 있다.
쉽게 설명하기 위해 많은 내용을 생략했다. 자세한 내용은 위키를 참고하자.
튜링 머신(Turing machine)
결정론적 튜링 머신(deterministic Turing machine)
컴퓨터는 정말 수많은 일들과 복잡한 일들을 한다. 프로그램을 실행시키고 복잡한 연산들을 수행하기도 하며, 컴퓨터 자원들을 스스로 효율적으로 관리하기도 한다. 그 중에서도 컴퓨터가 하는 가장 핵심적인 기능은 정해진 명령에 따라 원하는 값을 바꿔주는 기능 인데, 이처럼 정해진 명령표(예를 들어 헤드를 한 칸 움직여라 or 테이프의 값을 바꿔라 같은)에 따라 원하는 일을 수행하는 가상의 기계를 튜링 머신 이라 한다. 튜링 머신은 실제로 존재하는 것이 아니며, 전산학상의 개념으로 추상화 시킨 것을 튜링 머신이라 한다.
여기 결정론적 튜링 머신이 어떻게 작동하는지 쉽게 영상으로 보여주는 영상이 있다.
이 링크 를 참고하자.
P 문제에 대해서 다시 한번 정리하면, P 문제는 (일반적인 컴퓨터와 같은) 튜링 머신이 다항 시간내에 풀어낼 수 있는, 쉬운 문제를 의미한다. 예시로는 정렬 문제가 있다.
비결정론적 튜링 머신(non-deterministic Turing machine)
비결정론적 튜링 머신(nondeterministic Turing machine, NTM)은 튜링 머신에서 특정 상태에서 움직일 수 있는 상태의 개수가 하나로 정해져 있지 않은 경우를 말한다.
라고 위키 백과에 정의되어 있다.
하지만 너무 어려우니 쉽게 설명해보면, 특정 입력 값이 주어진 문제의 해답인지를 검사하는 장치를 말한다. 예를 들어보자.
그래프가 주어졌을 때 그래프의 모든 점을 정확하게 한번씩만 지나는 경로가 존재하는가?
위와 같은 문제가 주어졌다고 하자(보통 이를 해밀턴 경로 문제라 한다.). 이 문제에 대해 어떤 경로를 입력으로 준다면, 비결정론적 튜링머신은 이게 정답인지 아닌지 알려준다. 그렇다면 다시 NP문제로 돌아가서, 비결정론적 튜링머신이 주어진 입력이 정답인지 아닌지 계산하는데 다항시간이 걸린다고 하면, 이는 NP 문제라고 한다. 다시 말하면, 결정론적 튜링머신으로 다항 시간에 풀어낼 수 없는 문제들을 NP 문제라고 한다.
co-NP 문제
co-NP 문제에 대해서 쉽게 이해하기 위해, 위에서 언급했던 다시 해밀턴 경로를 예로 들어보자. 이 문제에서 그래프의 모든 점을 정확하게 한번씩만 지나는 경로를 찾으면, 이에 질문에 대한 답은 Yes라는 것을 비결정론적 튜링 머신은 알 수 있다. 하지만 한 번씩이 아니라 한 점을 두 번 지나는 경로를 찾았다고 이에 대한 답이 “한 번씩만 지나는 경로가 존재하지 않는다”가 될 수 없다.(한 점을 두 번 지나는 경로가 있다고 해서 모든 점을 한 번씩 지나는 경로가 없다는 것은 말이 안되니까) 다시 말해서, No라는 답을 다항시간 안에 확인 할 수 있게 해주는 “적당한 모범답안”이 존재하지 않고 Yes라는 답을 다항시간 안에 확인 할 수 있게 해주는 “적당한 모범답안”이 존재한다면 이는 NP 문제이다. 하지만 이를 반대로 생각했을때, No라는 답을 다항시간 안에 확인할 수 있게 해주는 “적당한 모범답안”이 존재한다면, 즉, 그래프의 모든 점을 정확하게 한번 씩만 지나는 경로는 없는가? 라는 문제가 있다면, 이는 co-NP 문제라고 할 수 있겠다.
NP-난해(NP-hard) 문제
요약
적어도 NP문제 보다는 어려우며, “모든” NP 문제를 다항 시간 내에 어떤 문제 A로 환원(reduction)할 수 있다면, 그 A 문제를 NP-난해(NP-hard) 문제라고 한다.
환원(reduction)
환원을 가지고 NP-난해 문제를 설명 했었으니, 이제 환원에 대해서 설명해보자.
환원은 두 난이도를 비교할 때 자주 사용되는 기법이다. 다음과 같은 두 문제가 있다고 해보자.
문제 A: 주어진 n개의 숫자를 크기 순서로 정렬하는 문제
문제 B: 주어진 n개 숫자의 중간값을 계산하는 문제
어떤 사람이 문제 A를 쉽게 풀 수 있다면, 그 사람은 문제 B도 쉽게 풀 수 있는 것이 당연하다. 왜냐하면 주어진 숫자들을 정렬하고 나면, 그 중 정 가운데에 있는 수를 뽑기만 하면 그것이 중간값이 될 것이기 때문이다. 이와 같은 일이 벌어진다면, 문제 B를 문제 A로 환원시킬 수 있다(reducible)고 표현하며, 문제 A의 난이도는 문제 B의 난이도보다 어렵다는 것을 알 수 있다. 즉, “환원한다” 는 것은 쉬운 문제(중간값 계산 문제)에서 어려운 문제(정렬 문제)로 바꿀 수 있다는 의미이다.
또 다른 좀 더 쉬운 예를 들어보자. 곱셈은 사실 덧셈만 알고 있어도 된다. 7*8은, 7을 8번 더한 것과 같고, 4*4은 4를 4번 더한 것과 같다. 그래서 사실 덧셈만 무지하게 빠르게 잘한다면 곱하기를 외울 필요가 없다. 결국, 곱셈 문제는 덧셈 문제로 환원할 수 있다고 하는 것이다. 그래서 결국 덧셈 문제는 곱셈 문제보다는 “어렵다”라고 정의하는 것이고, 덧셈 문제를 해결할 수 있다면 곱셈 문제도 당연히 해결할 수 있다.(곱셈은 단순히 덧셈을 여러번 하면 되니까)
다시 NP-난해의 설명으로 돌아가면, 이 세상에 있는 모든 NP문제를 다항 시간내에 어떤 문제로 환원할 수 있다면, 그 문제를 NP-난해 라고 하는 것이고, NP-난해 문제는 이 세상에 있는 모든 NP 문제보다 “어렵다”라고 정의할 수 있는 것이다.
“어렵다”라는 개념을 쉽게 이해하기 위해 다시 곱셈과 덧셈을 생각해보자. 상식적으로 생각하기엔 곱셈이 더 어려워 보이지만, 사실은 곱셈은 덧셈이 기반이 된다면 빠르게 할 수 있는 연산이다. 하지만 덧셈 그 자체에 대한 개념은 생각해내는거 자체가 굉장히 까다로운 것이다. 그래서 P-NP 개념에서는 덧셈을 더 “어렵다”고 정의하는 것이고, 환원은 쉬운 문제(곱셈)에서 어려운 문제(덧셈)으로 바꾼다는 개념이다.
예시
NP-hard에는 두가지 유형이 있다. NP에 속하는 NP-hard문제, NP에 속하지 않는 NP-hard 문제. NP에 속하는 NP-hard문제는 NP-완전 문제임으로 나중에 설명하도록 하고, NP에 속하지 않는 NP-hard 문제에는 어떤 예시가 있는 지 살펴보자.
정지 문제(Halting Problem)
정지 문제는 간단하게 설명하면, 문제는 명확하게 제시되어 있지만, 풀 수 없는 문제라고 증명된 문제이다.
나무 위키에서 너무나도 쉽게 정의해 놓았다.
좀 더 부가적인 설명을 하자면, exit라는 “a 프로그램에 i 입력을 먹이면 알고리즘이 끝날 것인가 무한루프에 빠질 것인가”라는 함수가 이미 존재한다고 가정한 후, 이 가정이 모순적임을 증명하며 exit따위는 존재하지 않는다, 즉, 정지 문제를 해결할 문제 따위는 존재하지 않는다를 증명한 것이다(이를 귀류법을 통한 증명이라 한다.)
NP-완전(NP-complete) 문제
NP 난해 문제에도 포함되며, NP 문제에도 포함된다면 이를 NP-완전(NP-complete) 문제라고 한다. NP 문제들 중에 풀 수 있는 가장 어려운 문제라고도 할 수 있겠다.
NP 난해 문제는 모든 NP 문제보다 어려운 문제라고 했으며, NP 문제는 비결정론적 튜링머신으로 “풀 수 있는” 문제라고 했다. 즉, NP-완전 문제는 “풀 수 있는” NP문제 중 가장 어려운 문제이다.
이 말은 즉슨 NP-완전 문제 중 단 하나라도 다항 시간 내에 풀어낼 수 있다면, 환원(reduction)에 의해 모든 NP를 다항시간에 풀어낼 수 있으므로(왜냐면 모든 NP문제는 NP-complete 문제보다는 쉬우니까) P=NP인 것을 증명할 수 있다!
좀 더 부가 설명을 하자면, NP문제에 속하는 NP-hard문제(NP-완전 문제)와 NP문제에 속하지 않는 NP-hard 문제의 차이는 결정가능한(decidable)지의 여부이다.
결론
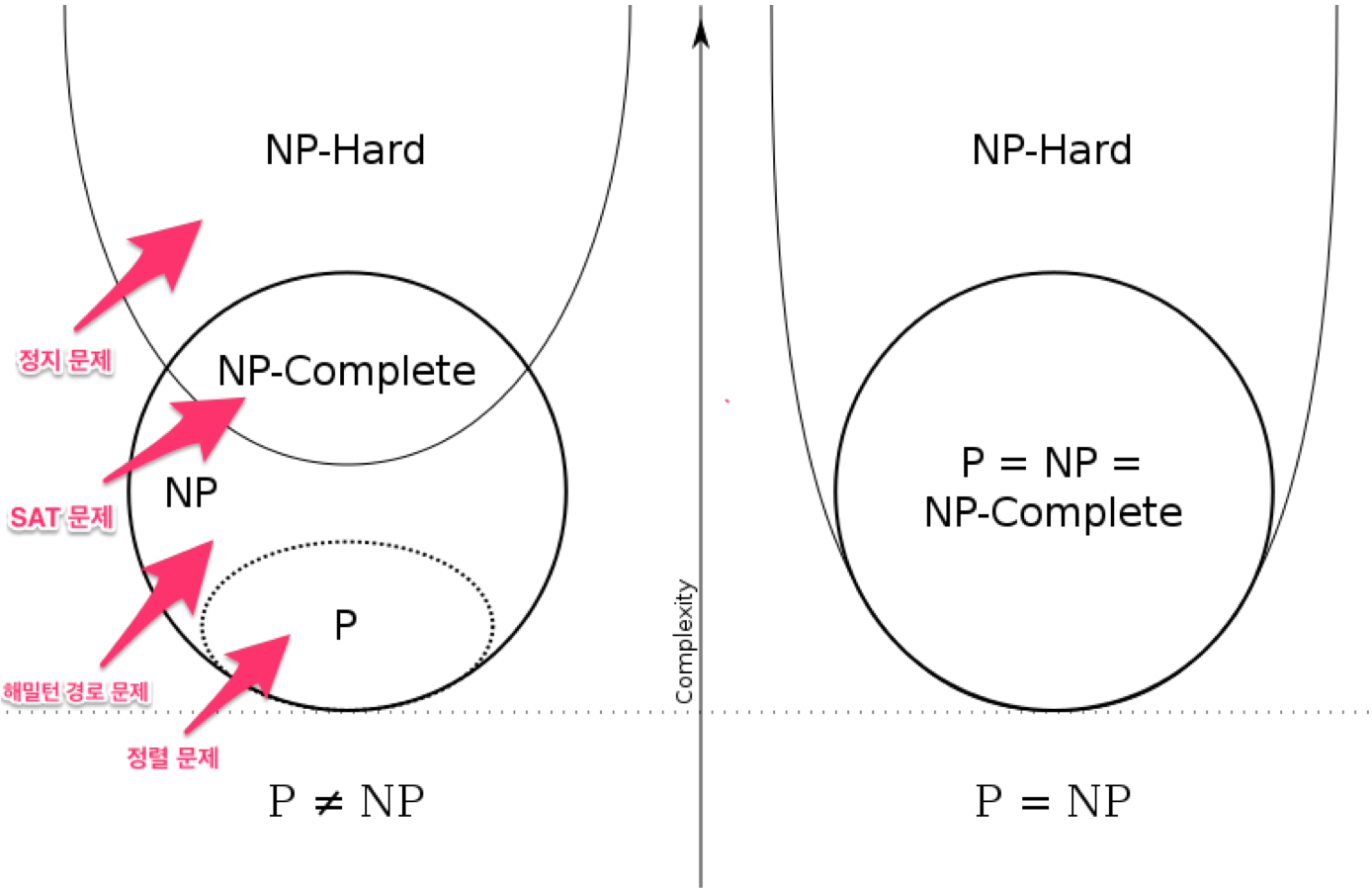
다이어그램이 두 개인 이유는, 아직 P=NP인지 P!=NP인지 증명이 안되었기 때문이다.
이제까지 설명한 것을 바탕으로, 위의 다이어그램을 보며 난이도 순으로 다시 한번 설명해보자, P 문제는 정렬 문제와 같이 결정론적 튜링 머신으로 쉽게 풀어낼 수 있는 문제들을 말한다. NP 문제는 비 결정론적 튜링머신으로 다항시간 내에 풀어낼 수 있는, 즉, 시간이 오래 걸리는 문제들을 말한다. 그리고 모든 NP문제들을 이 어떤 문제 A로 환원(reduction)할 수 있고 환원한 문제를 해결할 수 있다면, 이 문제 A는 NP-완전 문제(NP-complete)이라 하고(정확히 말하면 NP-난해 문제이자 NP-완전문제), 환원한 문제를 해결할 수 없다면 이를 NP-난해(NP-hard)라고 한다.
P = NP 또는 P != NP 증명의 의의
P = NP 또는 P != NP를 증명한다는 것은 약 12억의 상금과 튜링상 수상 뿐만 아니라 그 이상의 의미를 가진다. P = NP라고 증명이 된다면, 현재 NP라고 일컬어지는 모든 문제들이(길찾기, 방문 판매 알고리즘 등) 전부 P문제로서 풀릴 수 있다는 의미이다. 즉, 방문 판매 알고리즘 같이 무조건 시간이 오래걸리는 방법으로 풀 수 밖에 없다고 생각되는 것도 방법만 잘 찾는다면 다항 시간 내에 뚝딱 해결할 수 있다는 것이다. 반대로 생각해서 P != NP가 증명이 된다면, 수많은 NP 문제들이 P 문제로 환원될 수 없다고 증명됐으니 더 쉬운 방법(P 문제로 환원할 방법)을 찾으려고 애쓸 필요가 없다. 즉 이건 어려운 문제니까 쉬운 문제로 만드려고 해봤자 소용 없다는 걸 알게 되는 것이다.(헛수고를 줄여준다.)