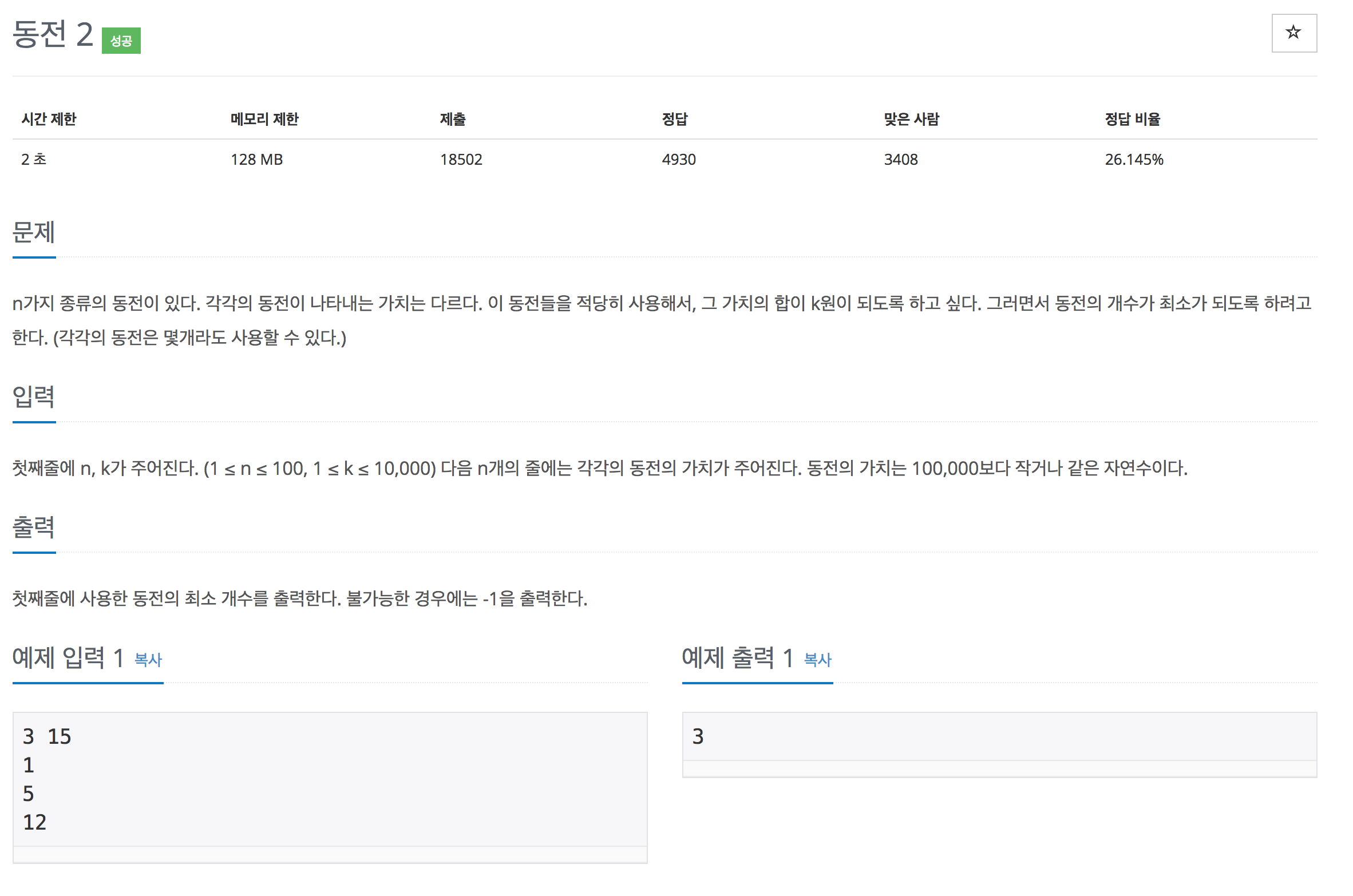
다이나믹 프로그래밍(Dynamic Programming, DP) 문제이다.
절차
- 가장 먼저 우리가 구하고자 하는 해답 함수를 정의한다.
- coin(n, k) 함수의 정의 : n번째 동전부터 마지막 동전(N-1번째 동전)을 가지고 k를 만들 수 있는 최소 경우의 수. 즉, 해답은 coin(0,K)가 된다.
- 해답 함수에 대한 점화식을 정의한다.
- 점화식:
coin(n,k) = min(coin(n+1, k), coin(n, k-cost[n])+1) - 자세한 설명은 소스 코드 주석에 첨부
- 점화식:
- 점화식이 주어진 조건을 벗어났을 경우를 정의한다.
- case 1.
k < 0: 동전 값은 양수이므로 k가 음수인 경우는 절대로 만들 수 없다. 따라서 무한한 값(INF)로 초기화 시켜준다. - case 2.
n == N이고k == 0(n==N의 의미는 N번째 동전부터 N-1번째 동전을 가지고 있다는 것인데, 이는 동전이 하나도 없다는 것과 같은 의미이다. ): 동전이 하나도 없을 때k == 0을 만들 수 있는 최소 경우의 수는 0이다.(즉, 동전을 하나도 선택하지 않는 방법이 최소) - case 3.
n == N이고k != 0: 동전이 하나도 없는데 0이 아닌 k를 만드는 것은 불가능하다. 따라서 무한한 값(INF)으로 초기화 시켜줌.
- case 1.
- 주어진 점화식을 memoization 시킨다(배열에 기록 한다). 만약 구하려는 n,k의 coin값이 이미 기록되어 있으면, 기록된 값을 반환한다.
소스코드 및 설명
설명은 주석에 첨부했습니다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// 절대 나올 수 없는 무한한 값으로 가정한다.
int INF = 10000000;
// memoization을 위한 101*10001(N의 최대값*K의 최대값) 크기의 mem 배열 선언 후 -1로 초기화
vector<vector<int>> mem(101, vector<int>(10001, -1));
// 입력받은 가격 값
vector<int> cost(101);
// 입력받은 N과 K
int N,K;
// coin의 정의 : n번째 동전부터 마지막 동전(N-1번째 동전)을 가지고 k를 만들 수 있는 최소 경우의 수. 즉, 해답은 coin(0,K)가 된다.
int coin(int n, int k)
{
// case 1. k < 0: 동전 값은 양수이므로 k가 음수인 경우는 절대로 만들 수 없다. 따라서 무한한 값(INF)로 초기화 시켜준다.
if(k < 0)
return INF;
// n == N이라는 것은 N번째 동전부터 N-1번째 동전을 가지고 있다는 것인데, 이는 동전이 하나도 없다는 것과 같은 의미이다.
// case 2. n == N 이고 k == 0: 동전이 하나도 없을 때 k==0을 만들 수 있는 최소 경우의 수는 0이다.(즉, 동전을 하나도 선택하지 않는 방법이 최소)
// case 3. n == N 이고 k != 0: 동전이 하나도 없는데 0이 아닌 k를 만드는 것은 불가능하다. 따라서 무한한 값(INF)으로 초기화 시켜줌.
if(n == N)
return (k == 0) ? 0 : INF;
if(mem[n][k] != -1)
return mem[n][k];
// 1. n번째 ~ N-1번째 동전을 가지고 k를 만들 수 있는 최소 경우의 수: coin(n, k-cost[n])+1
// 2. n+1번째 ~ N-1번째 동전을 가지고 k를 만들 수 있는 최소 경우의 수: coin(n+1, k)
// 위 두 가지 중에 더 최소가 되는 값이 coin(n,k)의 해답이 된다. 즉, 최소 경우의 수를 찾아내기 위해선 n번째 동전을 가지고 있는 것이 좋은지 아닌지 판단한다.
mem[n][k] = min(coin(n+1, k), coin(n, k-cost[n])+1);
return mem[n][k];
}
int main()
{
cin>>N>>K;
for(int i=0;i<N;i++)
cin>>cost[i];
int re = coin(0,K);
if(re == INF)
re = -1;
cout<<re<<endl;
return 0;
}