What is AVL tree?

AVL tree is represented as a prefix alphabet of the person who wrote the report related to it.
It is a tree to maintain the balance in the BST(Binary Search Tree).

Basic concepts

Binary Search Tree could be unbalanced, depending on inserting order. For example, Let 1,2,3,4,5 be inserted in the BST. It is no difference with list, That is, time complexity to search is just O(N). In other words, It would be disappeared the advantage of BST.
So, Maintaining the balance is really important in the BST. In the AVL tree, There are 2 basic rotation operations to maintain the balance.

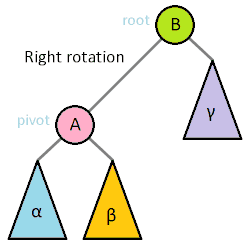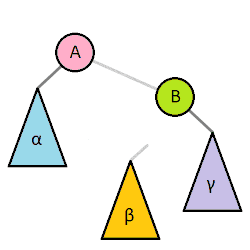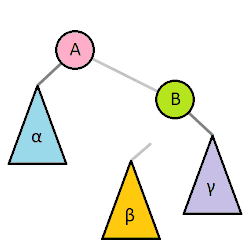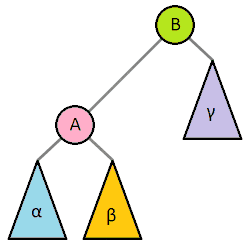
This gif file is described basic rotations well.

Right rotation

As above picture, left rotation makes every node moves one position to left from current position. The point is, Beta moves position to subtrees of the root from current position. The reason is that the Beta node value is larger than pivot node value.
Let’s implement it with a source code.

root->left = pivot->right;
pivot->right = root;
root = pivot;

Left rotation

Left rotation is the opposite in the implementation to right rotation. Let’s take a look at the implementation of source code as well.

root->right = pivot->left;
pivot->left = root;
root = pivot;

Double rotation

Given the explanations above are single rotation. But sometimes, it is not finished with only single rotation.
For example, Let’s insert 3,1,2 in order, Neither left rotation nor right rotation can solve the imbalance. Therefore, we have to conduct double rotation, which is composed of RL(Right Left) and LR(Left Right) rotation.

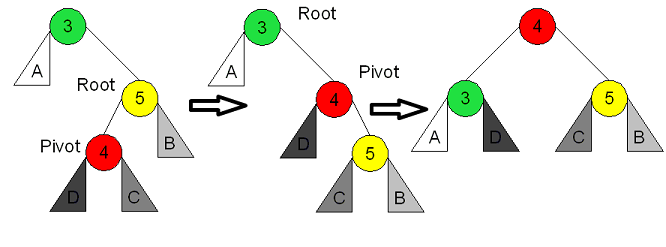
RL(Right-Left) rotation.

It is rotation that processes the right rotation and left rotation in sequence. Let’s take a look at the case that 3,5,4 is inserted in order. First, let 4 be as pivot and rotate right. And, let 5 be as pivot and rotate left. Eventually, the tree would be balanced.
This following picture show these processes.

LR(Left-Right) rotation.

The LR rotation is simply opposite concepts to RL rotation.

Balance Factor

How can we know whether the parts of tree is balanced or not? How can we decide which rotation is appropriate? We can use the Balance Factor for it. Balance factor is as follows.

Balance Factor = The height of the left tree - The height of the right tree.

And then, The unbalanced state of the tree could be represented as the following picture.

1. BF > 1,The value of the new node is smaller than the value of the left node.
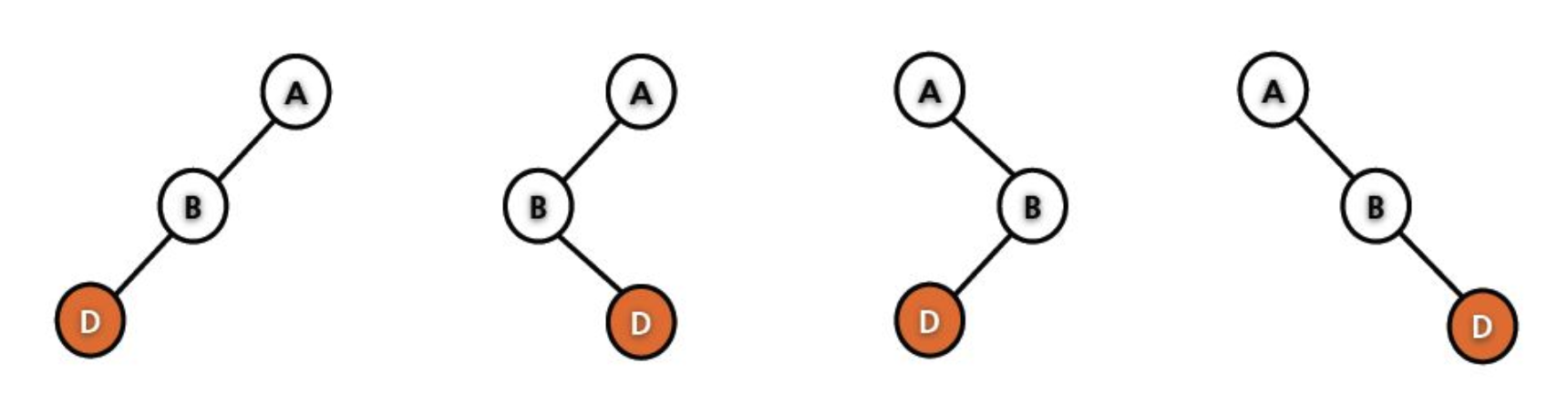
2. BF > 1, The value of the new node is larger than the value of the left node.
3. BF < -1, The value of the new node is smaller than the value of the right node.
4. BF < -1, The value of the new node is larger than the value of the right node.

In each state of the tree, We have to conduct the rotation like this:

1. Right rotation (pivot is the B)
2. Left rotation (pivot is the D) and Right rotation.(pivot is the B)
3. Right rotation (pivot is the D) and Left rotation.(pivot is the B)
4. Left rotation (pivot is the B)

Insertion of the AVL tree

If you understand the explanations so far, insertion process of AVL Tree would be so easy.
Let’s just take it step by step.

1. Insert the node as BST tree.
2. Update the height value of the visited node.
3. Balance the tree through the rotations (with balance factor).

Note that the height of nodes have to be updated after the rotation is conducted.

That’s all. It seems to be quite easy, but the implementation is not really.

Time Complexity (Big O notation)

Both the time complexity of insertion and deletion are O(logN).

Source code (C++)

#include <iostream>

using namespace std;

class Node
{
public:
    Node* left;
    Node* right;

    int value;
    int height;

    Node(int value)
    {
        this->value = value;
        left = right = nullptr;
        height = 1;
    }
};
class AVL
{
public:
    int getHeight(Node* node)
    {
        if(node == nullptr)
            return 0;

        return node->height;
    }
    Node* updateHeight(Node* node)
    {
        node->height = 1 + max(getHeight(node->left), getHeight(node->right));
        return node;
    }
    Node* insert(Node* root, int value)
    {
        if(root == nullptr)
            return new Node(value);

        if(root->value < value)
            root->right = insert(root->right, value);
        else if(root->value == value)
        {
            cout<<"value: "<<value<<" No duplicate vertex allowed."<<endl;
            return root;
        }
        else
            root->left = insert(root->left, value);

        root = updateHeight(root);

        int balance_factor = getHeight(root->left) - getHeight(root->right);

        // LR rotation
        if(balance_factor > 1 && root->left->value < value)
        {
            root->left = leftRotate(root->left);
            return rightRotate(root);
        }
        // RR rotation
        else if(balance_factor > 1 && root->left->value > value)
            return rightRotate(root);
        // LL rotation
        else if(balance_factor < -1 && root->right->value < value)
            return leftRotate(root);
        // RL rotation
        else if(balance_factor < -1 && root->right->value > value)
        {
            root->right = rightRotate(root->right);
            return leftRotate(root);
        }

        return root;
    }

    Node* leftRotate(Node* root)
    {
        Node* x = root->right;
        Node* t = x->left;

        root->right = t;
        x->left = root;

        // update height
        x = updateHeight(x);
        root = updateHeight(root);

        return x;
    }
    Node* rightRotate(Node* root)
    {
        Node *x = root->left;
        Node *t = x->right;

        root->left = t;
        x->right = root;

        // update height
        root = updateHeight(root);
        x = updateHeight(x);

        return x;
    }
    void printAll(Node* root)
    {
        if(root->left != nullptr)
            printAll(root->left);

        cout<<root->value<<" ";

        if(root->right != nullptr)
            printAll(root->right);
    }
};
int main()
{
    AVL avl;
    Node* root=nullptr;

    root = avl.insert(root, 10);
    root = avl.insert(root, 20);
    root = avl.insert(root, 30);
    root = avl.insert(root, 40);
    root = avl.insert(root, 50);
    root = avl.insert(root, 25);

    avl.printAll(root);

    return 0;
}