세그먼트 트리(Segment Tree)란?
A 배열의 부분 합을 구할 때 A 배열이 계속해서 바뀔 수 있다고 할때, 부분 합을 트리구조에 저장함으로서 O(logN)의 속도로 A 배열의 부분 합을 빠르게 구할 수 있게 한다.
세그먼트 트리 만들기.
다음과 같은 구조로 트리를 만듭니다. 부모 노드의 값은 자식 노드 값들의 합이고, 리프 노드는 A 배열의 각 요소들입니다.
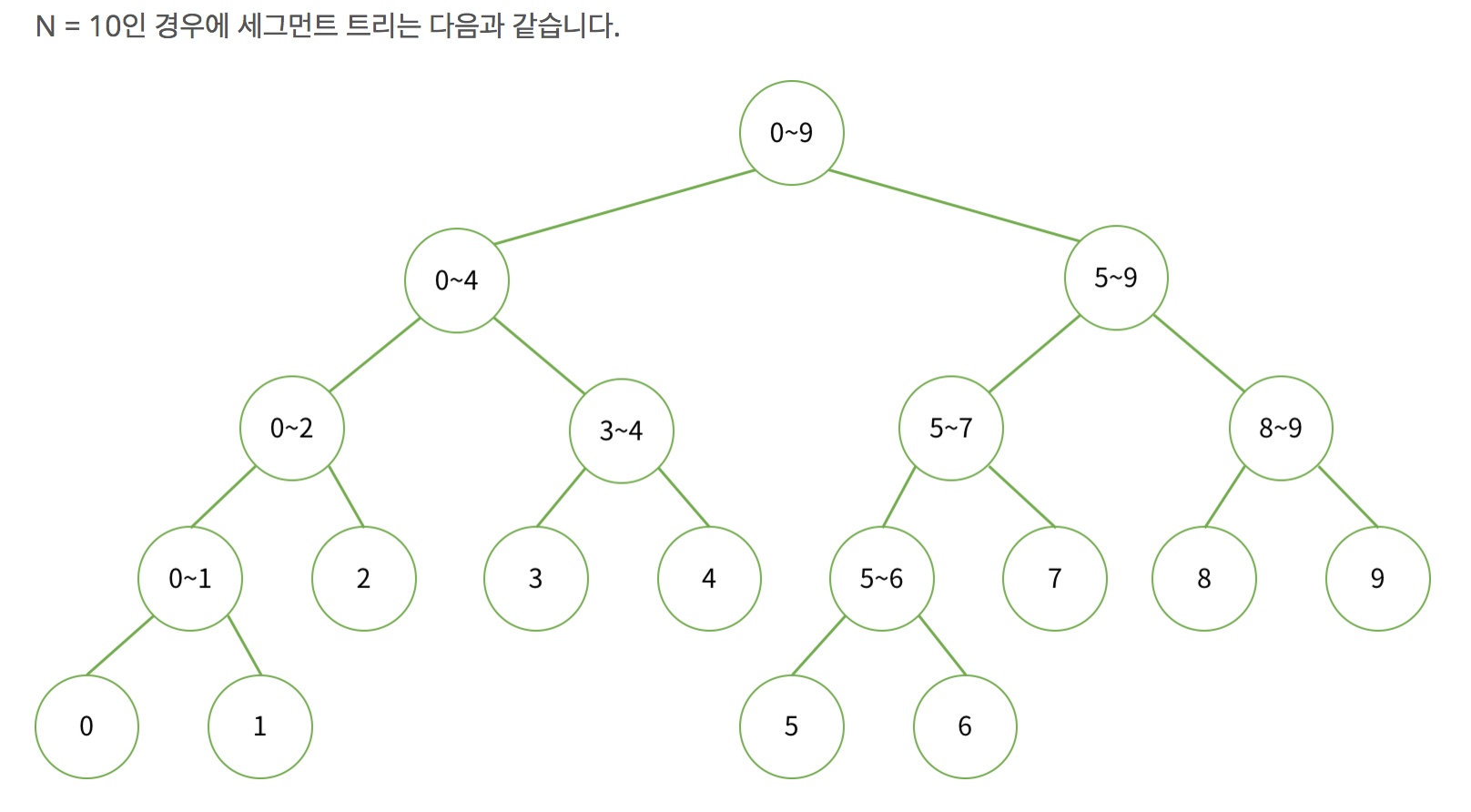
A 배열의 크기가 N이라 하면, 리프 노드의 개수는 N이 되므로 이 트리의 높이 H는 [logN]이 되고, 배열의 크기는 2^(H+1) 입니다.
이 트리는 배열을 이용해서 데이터들을 관리합니다.
N이 10이라고 할 때 각 노드의 인덱스 값은 다음과 같습니다.
위와 그림은 1부터 시작했지만, 저는 0부터 시작하는게 편하므로 0부터 시작한 것을 기준으로 설명 하겠습니다.
루트 노드의 인덱스는 0이고, 배열의 i번째 요소의 자식노드의 값은 i2+1, i2+2에 위치합니다.
트리를 구성하기 위해 재귀로 값을 지정합니다. 구현 코드는 다음과 같습니다.
#include <math.h>
int *tree;
int A[10] = {1,4,2,3,5,1,2,4,5,3};
long long init(int index, int start, int end)
{
if(start == end)
tree[index] = A[start];
else
tree[index] = init(index*2+1, start, (start+end)/2) + init(index*2+2, (start+end)/2 + 1, end);
return tree[index];
}
void main()
{
int N=10;
int h = ceil(log2(N));
int tree_size = 1 << (h+1);
tree = new long long[tree_size];
init(0, 0, N-1);
delete[] tree;
}
이제 세그먼트 트리를 만들었으니, 특정 범위[left, right]의 합을 구하는 sum함수를 구현하겠습니다.
탐색 범위인 [start, end]에서 구하려는 합의 범위인[left, right] 구간의 관계는 다음과 같은 4가지 경우가 있습니다.
- [left, right] 범위가 [start, end]와 전혀 겹치지 않는 경우
- [start, end] 범위가 [left, right]에 완전히 속해 있는 경우
- [left, right] 범위가 [start, end]에 완전히 속해 있는 경우
- 그 외의 경우 (범위가 일부분 겹치는 경우)
1번의 경우는 찾으려는 범위가 전혀 겹치지 않으므로, 더 이상 자식 노드로 탐색할 필요없으므로 그냥 0을 반환하면 됩니다.
2번의 경우에는 탐색 범위가 구하려는 전체 범위에 포함되므로, 하위 노드를 탐색할 필요 없이 start에서 end까지의 합인 tree[index]를 반환하면 됩니다.
3, 4번의 경우에는 여전히 하위 범위를 탐색하며 그 범위가 1, 2번의 경우에 해당되는지 아니면 더 하위범위를 탐색할건지 판단해야 하므로, 재귀 호출을 실행합니다.
구현 소스는 다음과 같습니다.
long long sum(int index, int start, int end, int left, int right)
{
if( start > right || end < left ) // case 1
return 0;
else if( start >= left && end <= right) //case 2
return tree[index];
else // other case
{
int mid = (start+end)/2;
return sum(2*index+1, start, mid, left, right) + sum(2*index+2, mid+1, end, left, right);
}
}
이번엔 A 배열 중 changed_index 번째 값을 value로 변경 시킬 경우에, 세그먼트 트리(tree 배열)는 어떻게 업데이트 해야할 지 알아봅시다.
- (value - A[changed_index])를 diff에 넣습니다.
- A[changed_index]에 value 값을 넣습니다.
- 탐색 범위를 나눠가며 노드가 리프 노드가 될때까지 (start == end) 다음과 같은 일을 수행합니다
- 변경하려는 changed_index가 탐색 범위[start, end]를 벗어났을 경우에, 더 이상 하위 노드를 탐색할 필요가 없으므로, 함수를 종료합니다.
- 위의 경우가 아닐 땐 해당되는 노드에 diff 값을 더해줍니다.
다음은 구현 소스입니다.
void update(int changed_index, ll diff, int index, int start, int end)
{
if(changed_index < start || changed_index > end)
return;
node[index] += diff;
if(start != end)
{
int mid = (start+end)/2;
update(changed_index, diff, index*2+1, start, mid);
update(changed_index, diff, index*2+1, mid+1, end);
}
}
위 소스들을 클래스화 시켜 백준 2042번 문제 - 구간 합 구하기를 푼 소스입니다.
#include <iostream>
#include <math.h>
typedef long long ll;
using namespace std;
class SegmentTree
{
private:
ll* nodes;
ll* A;
ll init(int index, int start, int end)
{
if(start == end)
nodes[index] = A[start];
else
nodes[index] =
init(2*index+1, start, (start+end)/2) +
init(2*index+2, (start+end)/2+1, end);
return nodes[index];
}
public:
SegmentTree(int N, ll* A){
int h = (int)ceil(log2(N));
int node_size = 1 << (h+1);
nodes = new ll[node_size];
this->A = A;
init(0, 0, N-1);
}
~SegmentTree(){
delete [] nodes;
}
ll getSum(int index, int start, int end, int left, int right)
{
//구하려는 범위가 밖에 있는 경우
if(left > end || right < start)
return 0;
else if(left <= start && right >= end)
return nodes[index];
int mid = (start+end)/2;
return getSum(index*2+1, start, mid, left, right) +
getSum(index*2+2, mid+1, end, left, right);
}
void update(int changed_index, ll diff, int index, int start, int end)
{
if(changed_index < start || changed_index > end )
return;
nodes[index] += diff;
if(start != end){
int mid = (start + end)/2;
update(changed_index, diff, index*2+1, start,mid);
update(changed_index, diff, index*2+2, mid+1,end);
}
}
};
int main()
{
ll A[1000001];
int N,M,K;
cin>>N>>M>>K;
for(int i=0;i<N;i++)
cin>>A[i];
int C = M+K;
SegmentTree st(N,A);
while(C--)
{
int a,b;
cin>>a>>b;
if(a == 1)
{
ll c;
cin>>c;
ll diff= c-A[b-1];
A[b-1]=c;
st.update(b-1, diff, 0, 0, N-1);
}
else if(a == 2)
{
int c;
cin>>c;
cout<<st.getSum(0, 0, N-1, b-1, c-1)<<endl;
}
}
}
그림 출처 –
https://www.acmicpc.net/blog/view/9